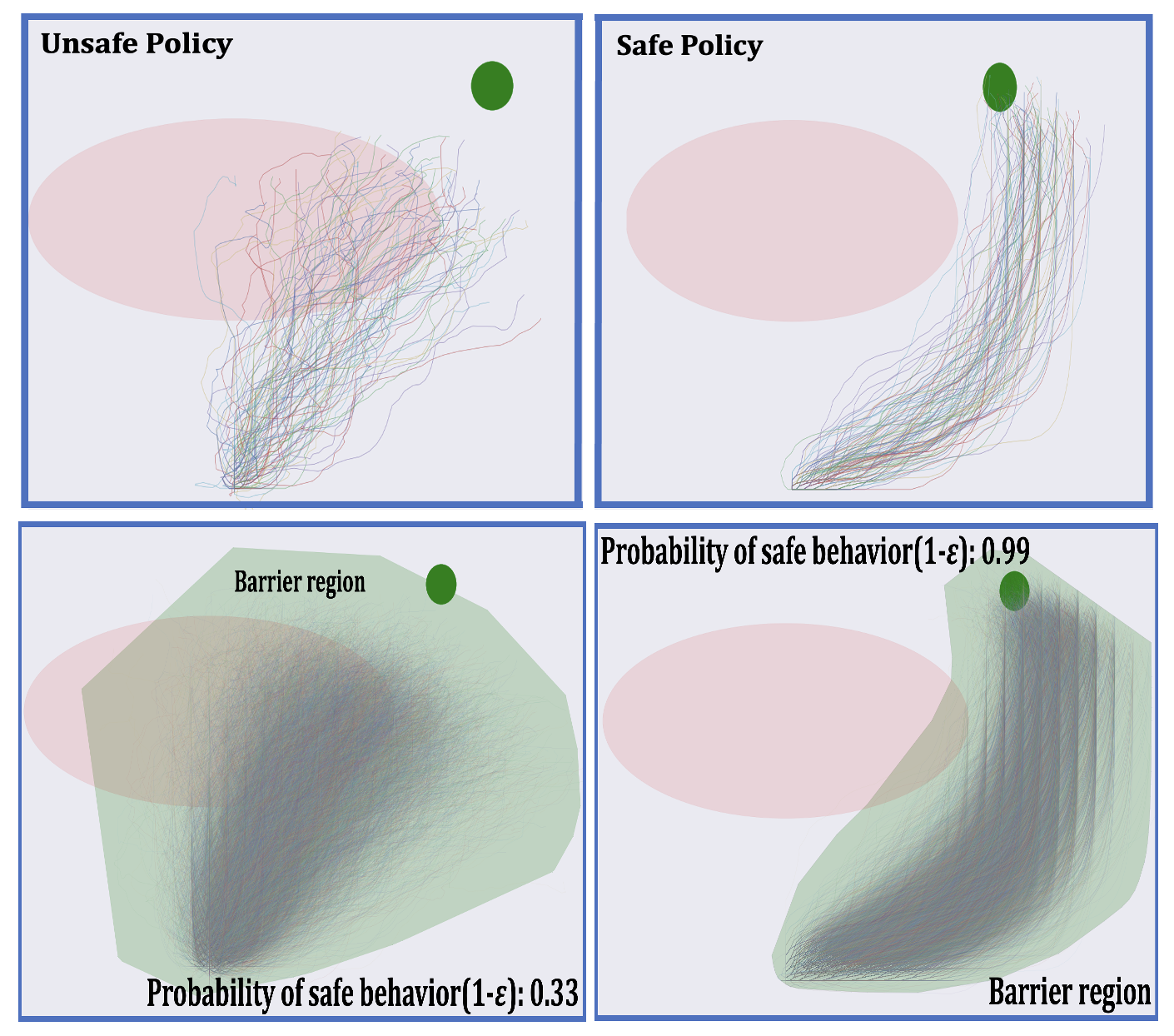
Probably Approximate Safe RL Policy [AAMAS-2024]
With the advancement of machine learning based automation in the current digital world, the problem of safety verification of such systems is becoming crucial, especially in safety-critical domains like self-driving cars, robotics, etc. Reinforcement learning (RL) is an emerging machine learning technique with many applications, including in safety-critical domains. The classical safety verification approach of making a binary decision on determining whether a system is safe or unsafe is particularly challenging for an RL system. Such an approach generally requires prior knowledge about the system, e.g., the transition model of the system, the set of unsafe states in the environment, etc., which are typically unavailable in a standard RL setting. Instead, this paper addresses the safety verification problem from a quantitative safety perspective, i.e., we quantify the safe behavior of the policy in terms of probability. We formulate the safety verification problem as a chance-constrained optimization using the technique of barrier certificate. We then use a sampling based approach called scenario optimization to solve the chance-constrained problem, which gives the desired probabilistic guarantee on the safe behavior of the policy. Our extensive empirical evaluation shows the validity and robustness of our approach in three RL domains.
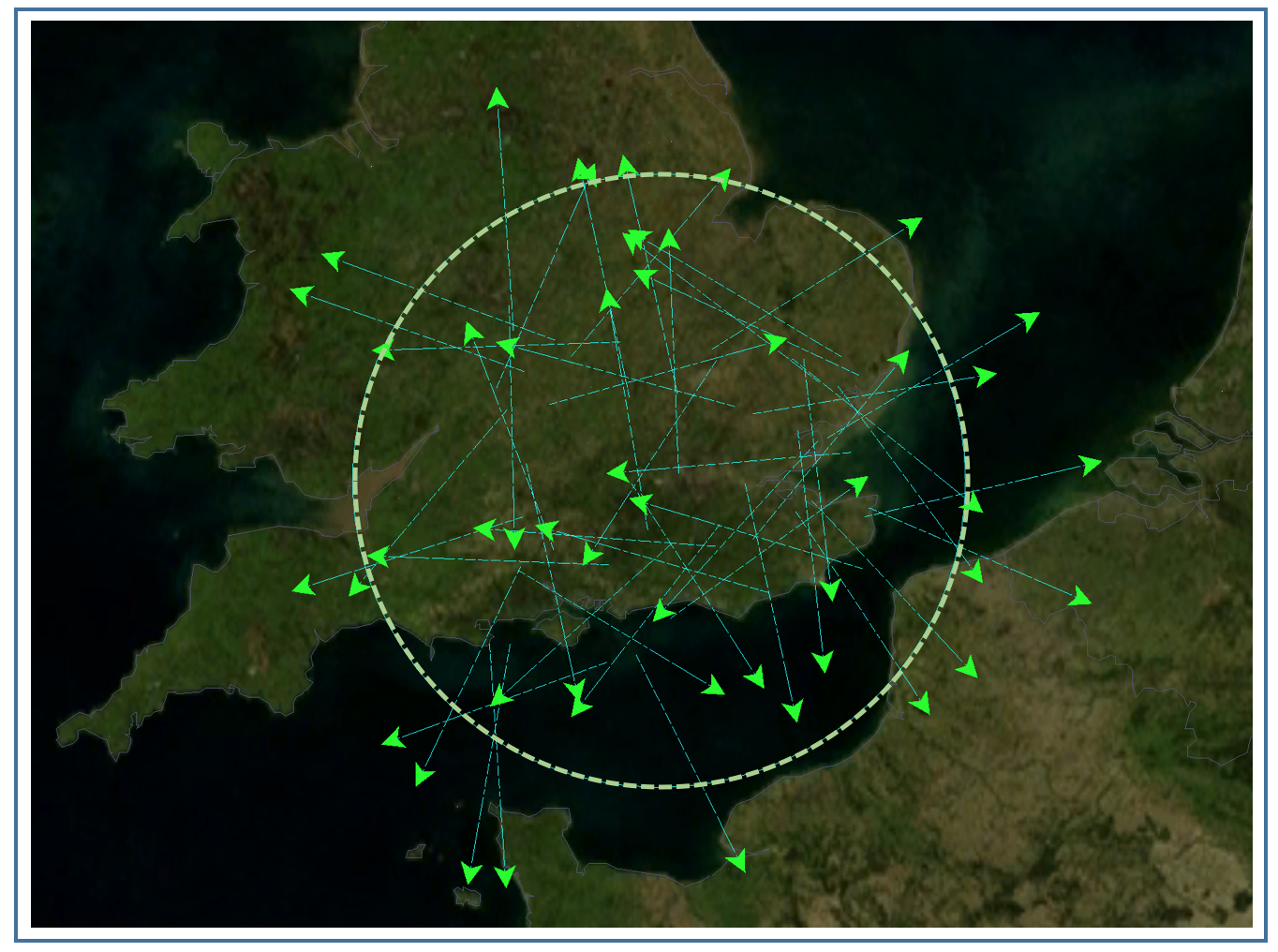
Air Traffic Control Problem [ICAPS-2021]
Many real world systems involve interaction among large number of agents to achieve a common goal, for example, air traffic control. Several model-free RL algorithms have been proposed for such settings. A key limitation is that the empirical reward signal in model-free case is not very effective in addressing the multiagent credit assignment problem, which determines an agent’s contribution to the team’s success. This results in lower solution quality and high sample complexity. To address this, we contribute (a) an approach to learn a differentiable reward model for both continuous and discrete action setting by exploiting the collective nature of interactions among agents, a feature commonly present in large scale multiagent applications; (b) a shaped reward model analytically derived from the learned reward model to address the key challenge of credit assignment; (c) a model-based multiagent RL approach that integrates shaped rewards into well known RL algorithms such as policy gradient, soft-actor critic. Compared to previous methods, our learned reward models are more accurate, and our approaches achieve better solution quality on synthetic and real world instances of air traffic control, and cooperative navigation with large agent population.
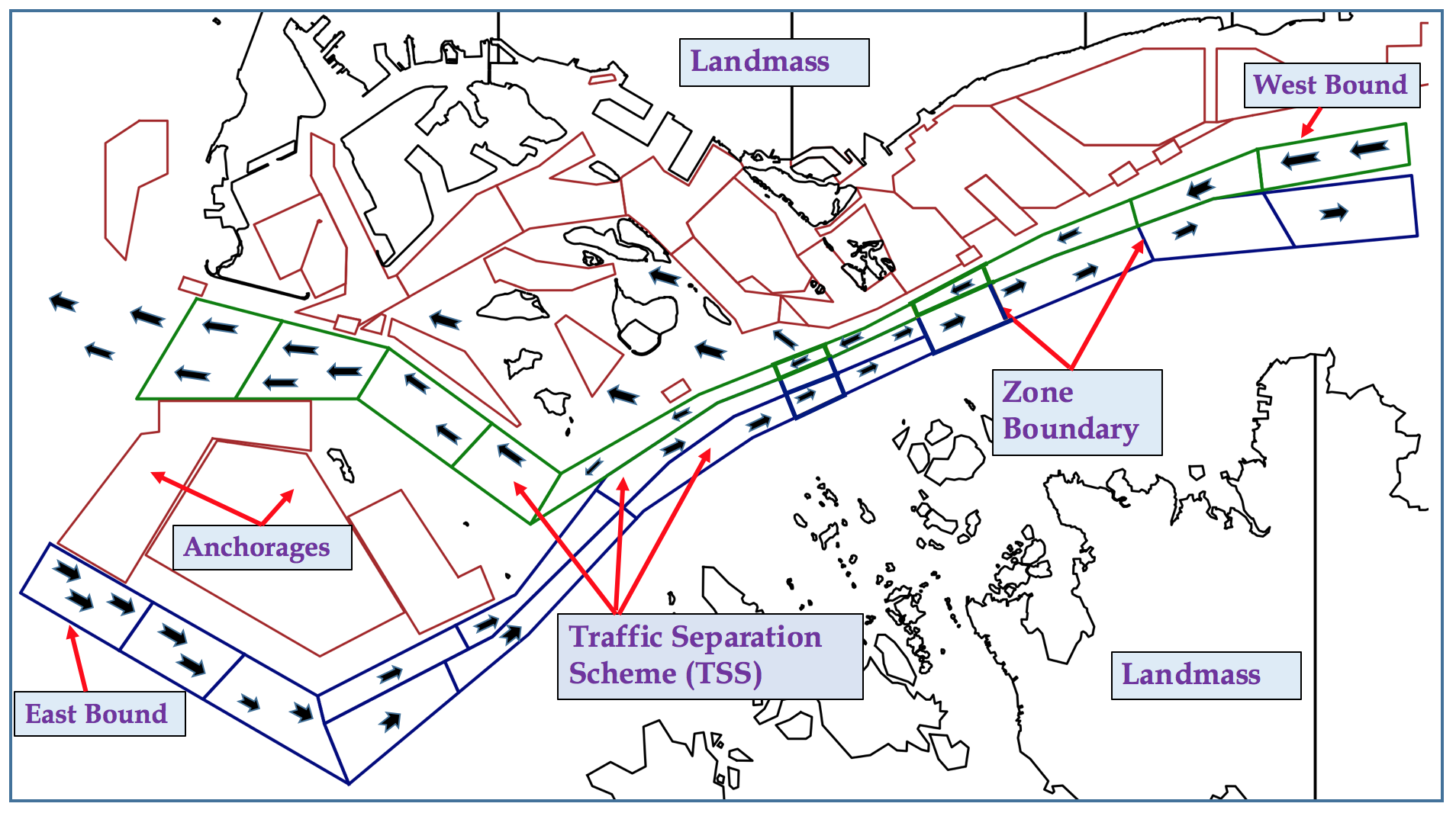
Maritime Traffic Management Problem [AAAI-19, AAMAS-20]
We address the problem of maritime traffic management in busy waterways to increase the safety of navigation by reducing congestion. We model maritime traffic as a large multiagent systems with individual vessels as agents, and the port authority as the regulatory agent. We develop a maritime traffic simulator based on historical traffic data that incorporates realistic domain constraints such as uncertain and asynchronous movement of vessels. We also develop a traffic coordination approach that provides speed recommendation to vessels in different zones. We exploit the nature of collective interactions among agents to develop a scalable policy gradient approach that can scale up to real world problems. Empirical results on synthetic and real world problems show that our approach can significantly reduce congestion while keeping the traffic throughput high.
Graph Based Optimization For Multiagent Cooperation [AAMAS-19]
We address the problem of solving math programs defined over a graph where nodes represent agents and edges represent interaction among agents. The objective and constraint functions of this program model the task agent team must perform and the domain constraints. In this multiagent setting, no single agent observes the complete objective and all the constraints of the program. Thus, we develop a distributed message-passing approach to solve this optimization problem. We focus on the class of graph structured linear and quadratic programs (LPs/QPs) which can model important multiagent coordination frameworks such as distributed constraint optimization (DCOP). For DCOPs, our framework models functional constraints among agents (e.g. resource, network flow constraints) in a much more tractable fashion than previous approaches. Our iterative approach has several desirable properties—it is guaranteed to find the optimal solution for LPs, converges for general cyclic graphs, and is memory efficient making it suitable for resource limited agents, and has anytime property. Empirically, our approach provides solid empirical results on several standard benchmark problems when compared against previous approaches.
Decision Making For Computational Sustainability [AAAI-16]
We address the problem of robust decision making for stochastic network design. Our work is motivated by spatial conservation planning where the goal is to take management decisions within a fixed budget to maximize the expected spread of a population of species over a network of land parcels. Most previous work for this problem assumes that accurate estimates of different network parameters (edge activation probabilities, habitat suitability scores) are available, which is an unrealistic assumption. To address this shortcoming, we assume that network parameters are only partially known, specified via interval bounds. We then develop a decision making approach that computes the solution with minimax regret. We provide new theoretical results regarding the structure of the minmax regret solution which help develop a computationally efficient approach. Empirically, we show that previous approaches that work on point estimates of network parameters result in high regret on several standard benchmarks, while our approach provides significantly more robust solutions.
Master's Thesis: Exploration and Realtime Mapping of an Obstacle-Prone Unknown Environment Using Swarm of Autonomous Mobile Robots
In my Master’s thesis, I worked on research concerning the application of Swarm Robotics for mapping an unknown area with unknown obstacles. The problem of mapping an unknown environment by a swarm of mobile robots is further divided into two classic problems of Multi-Robot Systems as Multi Robot Area Partitioning Problem and Area Exploration Problem. The robots considered here follow the basic Observe-Compute-Move model, which is also known as the CORDA Model. The robots are assumed to be a full compass and asynchronous timing models, and all of them remain active throughout the process. The robots considered here are all identical, with limited visibility and limited communication. There is no centralized control. Each robot executes the same algorithm in every cycle based on the local information. We solve the mapping problem in two modules. We propose a distributed algorithm for each module and also use concepts from computational geometry. In the first module, we solve the area partitioning problem where we divide the unknown area among the robots and assign each robot a part of the area. In the second module, each robot performs an exploration of the area assigned and simultaneously generates a topological graph(map) of the sub-area. Thus, by combining graphs of all sub-parts of the area, we get a map of the area. We simulate our proposed system with Player/Stage, and the map is constructed using Python’s graphics library.
| Software Simulation | Hardware Test |
|---|---|
